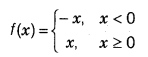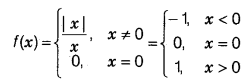Class 11 Notes Maths Probability

Class 11 Notes Maths Probability

  March 17, 2024    Schoolix

---

Random Experiment
An experiment whose outcomes cannot be predicted or determined in advance is called a random experiment.

Outcome

A possible result of a random experiment is called its outcome

Sample Space

A sample space is the set of all possible outcomes of an experiment.

Events

An event is a subset of a sample space associated with a random experiment. 

Types of Events

Impossible and sure events: The empty set Φ and the sample space S describes events. Intact Φ is called the impossible event and S i.e. whole sample space is called sure event.

Simple or elementary event: Each outcome of a random experiment is called an elementary event.

Compound events: If an event has more than one outcome is called compound events.

Complementary events: Given an event A, the complement of A is the event consisting of all sample space outcomes that do not correspond to the occurrence of A.

Mutually Exclusive Events
Two events A and B of a sample space S are mutually exclusive if the occurrence of any one of them excludes the occurrence of the other event. Hence, the two events A and B cannot occur simultaneously and thus P(A ∩ B) = 0.

Exhaustive Events
If E1, E2,…….., En are n events of a sample space S and if E1 ∪ E2 ∪ E3 ∪………. ∪ En = S, then E1, E2,……… E3 are called exhaustive events.

Mutually Exclusive and Exhaustive Events
If E1, E2,…… En are n events of a sample space S and if
Ei ∩ Ej = Φ for every i ≠ j i.e. Ei and Ej are pairwise disjoint and E1 ∪ E2 ∪ E3 ∪………. ∪ En = S, then the events
E1, E2,………, En are called mutually exclusive and exhaustive events.

Probability Function
Let S = (w1, w2,…… wn) be the sample space associated with a random experiment. Then, a function p which assigns every event A ⊂ S to a unique non-negative real number P(A) is called the probability function.
It follows the axioms hold

• 0 ≤ P(wi) ≤ 1 for each Wi ∈ S
• P(S) = 1 i.e. P(w1) + P(w2) + P(w3) + … + P(wn) = 1
• P(A) = ΣP(wi) for any event A containing elementary event wi.

Probability of an Event
If there are n elementary events associated with a random experiment and m of them are favorable to an event A, then the probability of occurrence of A is defined as

The odd in favour of occurrence of the event A are defined by m : (n – m).
The odd against the occurrence of A are defined by n – m : m.
The probability of non-occurrence of A is given by P(A¯) = 1 – P(A).

Addition Rule of Probabilities
If A and B are two events associated with a random experiment, then
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Similarly, for three events A, B, and C, we have
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(A ∩ C) – P(B ∩ C) + P(A ∩ B ∩ C)

Note: If A andB are mutually exclusive events, then
P(A ∪ B) = P(A) + P(B)

Read More

Class 11 Notes Maths Statistics

Class 11 Notes Maths Statistics

  March 17, 2024    Schoolix

---

 Measure of Dispersion

The dispersion is the measure of variations in the values of the variable. It measures the degree of scatteredness of the observation in a distribution around the central value.

Range
The measure of dispersion which is easiest to understand and easiest to calculate is the range.
Range is defined as the difference between two extreme observation of the distribution.

Range of distribution = Largest observation – Smallest observation.

Mean Deviation
Mean deviation for ungrouped data
For n observations x1, x2, x3,…, xn, the mean deviation about their mean x¯ is given byMean deviation for discrete frequency distribution

Let the given data consist of discrete observations x1, x2, x3,……., xn occurring with frequencies f1, f2, f3,……., fn respectively in caseMean deviation for continuous frequency distribution

where xi are the mid-points of the classes, x¯ and M are respectively, the mean and median of the distribution.

Variance
Variance is the arithmetic mean of the square of the deviation about mean x¯.
Let x1, x2, ……xn be n observations with \bar { x }

x¯ as the mean, then the variance denoted by σ2, is given by

Standard deviation
If σ2 is the variance, then σ is called the standard deviation is given by

Standard deviation of a discrete frequency distribution is given by

Standard deviation of a continuous frequency distribution is given by

Coefficient of Variation
In order to compare two or more frequency distributions, we compare their coefficient of variations. The coefficient of variation is defined as

Note: The distribution having a greater coefficient of variation has more variability around the central value, then the distribution having a smaller value of the coefficient 0f variation.

Read More

Class 11 Notes Maths Limits and Derivatives

Class 11 Notes Maths Limits and Derivatives

  March 17, 2024    Schoolix

---

 Limit

Let y = f(x) be a function of x. If at x = a, f(x) takes indeterminate form, then we consider the values of the function which is very near to a. If these value tend to a definite unique number as x tends to a, then the unique number so obtained is called the limit of f(x) at x = a and we write it as limx→af(x).

Left Hand and Right-Hand Limits
If values of the function at the point which are very near to a on the left tends to a definite unique number as x tends to a, then the unique number so obtained is called the left-hand limit of f(x) at x = a, we write it as

Existence of Limit

Some Properties of Limits
Let f and g be two functions such that both limx→af(x) and lim limx→ag(x) exists, then

Some Standard Limits

Derivatives
Suppose f is a real-valued function, then

Fundamental Derivative Rules of Function
Let f and g be two functions such that their derivatives are defined in a common domain, then

Some Standard Derivatives

Read More

Class 11 Relations and Function Notes

Class 11 Relations and Function Notes

  June 22, 2023    Schoolix

---

 

Relations and Functions

Ordered Pair
An ordered pair consists of two objects or elements in a given fixed order.

Equality of Two Ordered Pairs
Two ordered pairs (a, b) and (c, d) are equal if a = c and b = d.

Cartesian Product of Two Sets
For any two non-empty sets A and B, the set of all ordered pairs (a, b) where a ∈ A and b ∈ B is called the cartesian product of sets A and B and is denoted by A × B.
Thus, A × B = {(a, b) : a ∈ A and b ∈ B}
If A = Φ or B = Φ, then we define A × B = Φ

Note:

• A × B ≠ B × A
• If n(A) = m and n(B) = n, then n(A × B) = mn and n(B × A) = mn
• If atieast one of A and B is infinite, then (A × B) is infinite and (B × A) is infinite.

Relations
A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product set A × B. The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in A × B.
The set of all first elements in a relation R is called the domain of the relation B, and the set of all second elements called images is called the range of R.

Note:

• A relation may be represented either by the Roster form or by the set of builder form, or by an arrow diagram which is a visual representation of relation.
• If n(A) = m, n(B) = n, then n(A × B) = mn and the total number of possible relations from set A to set B = 2mn

Inverse of Relation
For any two non-empty sets A and B. Let R be a relation from a set A to a set B. Then, the inverse of relation R, denoted by R-1 is a relation from B to A and it is defined by
R-1 ={(b, a) : (a, b) ∈ R}
Domain of R = Range of R-1 and
Range of R = Domain of R-1.

Functions
A relation f from a set A to set B is said to be function, if every element of set A has one and only image in set B.
In other words, a function f is a relation such that no two pairs in the relation have the first element.

Real-Valued Function
A function f : A → B is called a real-valued function if B is a subset of R (set of all real numbers). If A and B both are subsets of R, then f is called a real function.

Some Specific Types of Functions
Identity function: The function f : R → R defined by f(x) = x for each x ∈ R is called identity function.
Domain of f = R; Range of f = R

Constant function: The function f : R → R defined by f(x) = C, x ∈ R, where C is a constant ∈ R, is called a constant function.
Domain of f = R; Range of f = C

Polynomial function: A real valued function f : R → R defined by f(x) = a0 + a1x + a2x2+…+ anxn, where n ∈ N and a0, a1, a2,…….. an ∈ R for each x ∈ R, is called polynomial function.

Rational function: These are the real function of type f(x)g(x), where f(x)and g(x)are polynomial functions of x defined in a domain, where g(x) ≠ 0.

The modulus function: The real function f : R → R defined by f(x) = |x|
or

for all values of x ∈ R is called the modulus function.
Domaim of f = R
Range of f = R+ U {0} i.e. [0, ∞)

Signum function: The real function f : R → R defined
by f(x) = |x|x, x ≠ 0 and 0, if x = 0
or

is called the signum function.
Domain of f = R; Range of f = {-1, 0, 1}

Greatest integer function: The real function f : R → R defined by f (x) = {x}, x ∈ R assumes that the values of the greatest integer less than or equal to x, is called the greatest integer function.
Domain of f = R; Range of f = Integer

Fractional part function: The real function f : R → R defined by f(x) = {x}, x ∈ R is called the fractional part function.
f(x) = {x} = x – [x] for all x ∈R
Domain of f = R; Range of f = [0, 1)

Algebra of Real Functions
Addition of two real functions: Let f : X → R and g : X → R be any two real functions, where X ∈ R. Then, we define (f + g) : X → R by
{f + g) (x) = f(x) + g(x), for all x ∈ X.

Subtraction of a real function from another: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, we define (f – g) : X → R by (f – g) (x) = f (x) – g(x), for all x ∈ X

Multiplication by a scalar: Let f : X → R be a real function and K be any scalar belonging to R. Then, the product of Kf is function from X to R defined by (Kf)(x) = Kf(x) for all x ∈ X.

Multiplication of two real functions: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, product of these two functions i.e. f.g : X → R is defined by (fg) x = f(x) . g(x) ∀ x ∈ X.

Quotient of two real functions: Let f and g be two real functions defined from X → R. The quotient of f by g denoted by fg is a function defined from X → R as

Read More