March 21, 2023 Schoolix
Motion In Straight Line
#
Kinematics
It is the
study of motion of physical bodies without going into the cause of motion.
→A
body is said to be in motion, if its position changes with time, with respect
to that observer.
NOTE:
Rest and Motion both are relative terms to each other.
# Distance
and Displacement
→Distance:
Actual path length traversed by a particle
It is a Scalar quantity.
→Displacement:
The shortest distance between the final and initial point.
It is a vector quantity.
NOTE:
|Displacement|≤ Distance.
# Average
Velocity and Average Speed
→Average
Velocity:
displacement/ total time taken
→Average Speed:
distance/ time interval
# Instantaneous
Velocity and Instantaneous Speed
→ It is defined as the velocity and speed
at a given instant of time
=
dx/dt
NOTE: Average
velocity when a body travels two equal distances with v1 and v2
= 2v1v2/v1+v2
→Average velocity when a body travels
with v1 and v2 for two equal time intervals
= v1+v2/2
# Acceleration
It is change of velocity divided by the time interval in which that occurred.
= △v/△t
→ Instantaneous acceleration is defined as the acceleration of a particle at a particular instant of time
= dv/dt
# General Analysis of Motion in a Straight Line
Case1: Motion with Variable Acceleration
→ Vf-Vi = ∫adt
→ Xf-Xi = ∫vdt
→ Vf2-Vi2/2 = ∫adx
Case 2: Motion with Variable Acceleration
→ v = u+at
→s = ut+at2/2
→ v2 –
u2 = 2as
# Retardation
When the speed of particle decrease or when the particle slows down, the motion is said to be under retardation. This may happen when acceleration is positive.
The necessary condition is that velocity(v) and acceleration)a) should be in opposite direction.
# Displacement in Tth second of Uniformly Accelerated Motion
= u +
a(2t-1)/2
# Freely Falling Objects (Motion Under Gravity)
A freely falling object is any object moving freely under the influence of gravity alone, regardless of its initial motion.
Any freely falling object experiences an acceleration directed downward, regardless of its initial motion.
→PROBLEM SOLVING STRATEGY
The problems based on motion under gravity are easy to solve, provided that you set up a suitable co-ordinate system at the start of the problem. The following steps may be helpful.
1) Origin Take the point of start of the object as origin.
2) Draw a vertical axis through point of projection, name this as y-axis.
3) Now the acceleration is a = -g
4) Take the moment of start as t=0 to write the expression for position and velocity at any time t.
5) The velocity at any time (t) is v = u+at or v = u-gt. Here u is the initial velocity (along with the sign) If the initial velocity is up, then u is a positive number else a negative number. Further if v comes out to be positive, then velocity is directed up else down.
6) The position at any time t or y=ut+at2/2 or y = ut-gt2/2. Again, if y is a positive number, the particle is above origin, else it is below origin.
7) Now you may apply the conditions on y or v to obtain the results as required in the given situation.
→IMPORTANT POINTS TO REMEMBER
1) T = 2u/g (Total flight time of the Object)
2) H(max) = u2/2g
# Graphical Representation of Motion in Straight Line
1) Position-Time Graph
i)Average velocity: For the graph shown, the particle moves from position x, to x2 when the time changes from t, to t₂. The average velocity in this interval AB is
V(av) = △x/△t
This shows that on x-t graph average velocity is represented by the slope of the line (chord) joining the initial and final points A and B corresponding to the initial and final time instants t, and t₂.
ii)Instantaneous velocity: The instantaneous velocity at A is the average velocity in the interval AB when B approaches A or At 0. The interval AB is infinitesimally small so that the average velocity in the interval is equal to the instantaneous velocity at A. When At → 0, B→ A, chord AB → tangent at A.
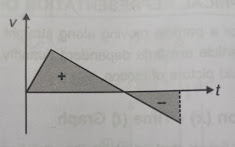
2) Velocity- Time Graph
i) Displacement and path length
On v-t graph, the displacement is represented by the area under the graph. In situations when the particle reverses its direction of motion the area below time axis will be taken negative
To find distance travelled (or path length) in the interval both the areas above and below time axis will be taken positive.
ii) Average Acceleration
Similar to the average velocity on x-t graph, the average acceleration on v-t graph, is represented by the slope of line AB joining initial and final points on graph.
a(av) = △v/△t =tanθ
iii) Instantaneous Acceleration
The slope of tangent to the graph at a point gives the instantaneous acceleration. In the v-t graph shown, at points A, B, C acceleration is positive, zero and negative respectively
3) Acceleration-Time Graph
i) Change in Velocity
In an interval of time, the change in velocity on a-t graph is represented by the area under the graph, taking the area above time axis as positive and the area below time axis as negative.
# Relative Velocity
→ Calculation of position, velocity and acceleration with respect to a frame
XBA =
XB – XA
VBA = VB
– VA
XA = Position of A w.r.t fixed point O.
XB = Position of B w.r.t fixed point O.
XBA = Position of B w.r.t A
So, with the above discussion we concluded that, if A and B are moving along the same direction then,
VAB = VA
– VB
VBA = VB
– VA
If A and B are moving in opposite directions
VAB = VA
– (-VB) = VA + VB = - VBA